Bruce’s Notes – Gases

Objective 1: Describe how a barometer and manometer can be used to measure gas pressure.

A sample of any substance existing as a gas can be described by four properties:

  • The number of moles of the gas (n)
  • The volume of the gas (V)
  • The temperature of the gas (T)
  • The pressure of the gas (P)

We are already familiar with temperature and volume, and the units used to measure them.  Let’s take a closer look at pressure.

Pressure:

Pressure is the amount of force that acts on a given area. Gases exert pressure because the individual particles (atoms or molecules depending on the gas) are in constant, high-speed motion.  These atoms or molecules strike the walls and surfaces of the containers they are in, causing pressure.  As the frequency and intensity of the molecular motion increases, causing more frequent or forceful collisions with the container walls, so does the pressure.  Gas pressures can be measured by a variety of devices.  The simplest ones are barometers and manometers.

Barometer

Barometers are used to measure the pressure of the atmosphere.  Figure 9.4 in OpenStax illustrates an early barometer.

This figure shows two barometers. The barometer to the left contains a shallow reservoir, or open container, of mercury. A narrow tube extends upward from the reservoir above the reservoir. This tube is sealed at the top. To the right, a second similar setup is shown with a reservoir filled with water. Line segments connect the label “vacuum” to the tops of the two narrow tubes. The tube on the left shows the mercury in the reservoir extending in a column upward in the narrow tube. Similarly, the tube on the right shows the water in the reservoir extending upward into the related narrow tube. Double-headed arrows extend from the surface of each liquid in the reservoir to the top of the liquid in each tube. A narrow column or bar extends from the surface of the reservoir to the same height. This bar is labeled “atmospheric pressure.” The level of the water in its tube is significantly higher than the level of mercury in its tube.

As the atmospheric pressure pushes down on the liquid, it is forced up into the tube.  Higher atmospheric pressure will push the liquid proportionally higher up into the tube.  The pressure can be expressed as the height (commonly inches or mm) the liquid is pushed up.  A more dense liquid such as mercury requires a shorter tube than a less dense liquid such as water, so mercury is commonly the liquid if choice.  The pressure of the air in the atmosphere is referred to as barometric pressure.

Normal atmospheric pressure is typically somewhere around 760 mm Hg or around 30 inches Hg.  If you look at a weather app on your phone, you might see it:

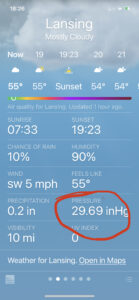
weather app screenshot from cell phone showing barometric pressure readout of 29.69 mm Hg

A barometric pressure of 29.69 in Hg is 754 mm Hg.

Standard atmospheric pressure at sea level is defined as 760 mm Hg.  The actual atmospheric pressure at a specific location varies and depends on the altitude and current weather conditions.

A manometer is used to measure of a gas other than the atmosphere.  OpenStax Figure 9.5 illustrates a manometer:

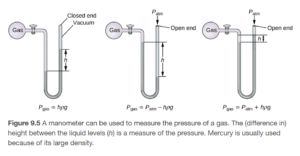
Three diagrams of manometers are shown. Each manometer consists of a spherical pink container filled with gas on the left that is connected to a U-shaped, sealed tube by a valve on its right. The top of the U aligns with the gas-filled sphere and the U, which extends below, contains mercury. The first manometer has a sealed tube. The sealed end to the upper right in the diagram is labeled “closed end” and “vacuum.” The mercury level is higher in the right side of the tube than in the left. The difference in height is labeled “h.” Beneath this manometer illustration appears the label P subscript gas equal sign h rho g. The second manometer has an open-ended tube, which is labeled “open end.” At this opening in the upper right of the diagram is the label P subscript atm. The mercury level is higher in the left side of the tube than in the right. This difference in height is labeled “h.” Beneath this manometer illustration appears the label P subscript gas equal sign P subscript atm minus sign h rho g. The third manometer has an open-ended tube and is similar to the second manometer except that the mercury level is higher in the right side of the tube than in the left. This difference in height is labeled “h.” Beneath this manometer illustration appears the label P subscript gas equal sign P subscript a t m plus h rho g.

Read the surrounding reading to Figure 9.5 in OpenStax – it provides a nice explanation!

The manometer has the gas whose pressure is being measured on one side and is open to the atmosphere on the other side.  The difference in height of liquid level on the two sides tells how many mm Hg lower or higher the gas pressure is than the barometric pressure.  If the barometric pressure is known (from a barometer) the gas pressure can then be calculated.  Closed end manometers are similar, but the gas pressure is measured against a vacuum rather than against barometric pressure.  See examples 9.3 and 9.4 on OpenStax Section 9.1 to see how manometers work.

Objective 2: Convert among various units of pressure, including torr, atmosphere, mm of Hg, and Pascals.

Units of pressure are defined in three general ways:

  1. Height of a column of liquid.  These are the units we just saw in the last objective, and include units such as mm Hg, inches Hg, inches H2O, and feet H2O.  A torr is another name for mm Hg (1 mm Hg=1 torr)
  2. Force/area units.  These include units like lb/in2 (pounds per square inch or psi) and Pascals (a Pascal or Pa is a Newton per square meter or N/m2)
  3. “atmospheres” or atm.  A standard atmosphere is defined as 760 mm Hg.

Table 9.1 in OpenStax list several other units of pressure and their conversions.

Pressure conversions

  • 1 mm Hg = 1 torr
  • 760 mm Hg = 760 torr = 1 atm = 101325 Pa
  • The Pascal (Pa) is the SI unit. 1 N/m2  = 1 Pa

Objective 2 Practice

Gas Laws

Objectives 3-6 cover gas laws, which are mathematical relationships between four properties of ideal gases:

  • Pressure (P)
  • Temperature (T)
  • Volume (V)
  • Number of moles (n)

We will discuss what is meant by an ideal gas later (when discussing gas theory).  The laws that apply to ideal gases are useful though, as they work well to predict gas properties at the temperatures and pressures we live with everyday.

Objective 3: Solve problems using Boyle’s law, Charles’ law, the combined gas law, and Avogadro’s Law.

Various laws summarize relationships between different combinations of the properties P,V,T, and n.  These laws are named after scientists who pioneered them or made contributions in this area:

  1. Boyle’s Law
  2. Charles’s Law
  3. Amonton’s law (or Gay-Lussac’s) Law
  4. Avogadro’s Law

In CHEM 151, you are not responsible for knowing which law is named after which scientist, but you should understand the relationships described by the laws and be able to apply them to solve problems.

Relationship of P and V (at constant T and n)

Boyle’s Law states that the volume of a fixed quantity (constant n) of gas at constant T is inversely proportional to the pressure.  In other words, if T and n do not change then P and V are inversely proportional (if P is doubled then V is halved, if V is made three times smaller then P is three times larger, etc ).  This can be shown in equation form as:

{{P}_{1}}{{V}_{1}}={{P}_{2}}{{V}_{2}}

where P1 and V1 are the initial pressure and volume and P2 and V2 are the final pressure and volume.

Example

A gas has a volume of 360.0 mL at 0.75 atm and 20 ° C.  What is the volume of the same gas at a pressure of 1.0 atm and 20° C?

The temperature does not change (20 ° C) and n does not change (the same gas).  Therefore,

{{P}_{1}}{{V}_{1}}={{P}_{2}}{{V}_{2}}

The following is given: P1=0.75 atm, V1= 360.0 mL, and P2 = 1.0 atm.  The problem asks for the final volume or V2.

Solving for V2, \frac{{{P}_{1}}{{V}_{1}}}{{{P}_{2}}}={{V}_{2}}.

Therefore, \frac{{{P}_{1}}{{V}_{1}}}{{{P}_{2}}}={{V}_{2}}=\frac{0.75atm(360.0mL)}{1.0atm}=270mL

Relationship of V and T (at constant P and n)

Charles’s Law states that the volume of a fixed quantity (constant n) of gas at constant P is directly proportional to the  absolute (Kelvin) temperature.  In other words, if P and n do not change then T and V are directly proportional (if V is doubled then T is doubled, if T is made three times smaller then V is three times smaller, etc ).  This can be shown in equation form as:

\frac{{{V}_{1}}}{{{T}_{1}}}=\frac{{{V}_{2}}}{{{T}_{2}}}

where T1 and V1 are the initial temperature and volume and P2 and V2 are the final temperature and volume.  Again, the temperature must be in Kelvin. If it did not, a problem could easily occur – negative Celsius temperatures (which often occur) would result in negative volumes, which are impossible!

Solving Charles’s Law problems are similar to the Boyle’s example problem shown above – given three of the four variables solve for the fourth.

Relationship of P and T (at constant V and n)

Amonton’s Law (also known as Gay-Lussac’s Law) is a similar relationship, stating that P and T are directly proportional at constant V and n:

\frac{{{P}_{1}}}{{{T}_{1}}}=\frac{{{P}_{2}}}{{{T}_{2}}}

Combined Gas Law

The previous three laws can all be contained in one law called the Combined Gas Law.  For a given gas sample (constant n):

\frac{{{P}_{1}}{{V}_{1}}}{{{T}_{1}}}=\frac{{{P}_{2}}{{V}_{2}}}{{{T}_{2}}}

The combined gas law is useful for 2 reasons:

  • It reduces the amount of laws to remember as it contains Boyle’s, Charles’s, and Amonton’s Laws.  For example:

Charles’s law applies at constant pressure, or P1=P2.

Starting with the combined law \frac{{{P}_{1}}{{V}_{1}}}{{{T}_{1}}}=\frac{{{P}_{2}}{{V}_{2}}}{{{T}_{2}}}, if P1=P2 then they can be cancelled, leaving \frac{{{V}_{1}}}{{{T}_{1}}}=\frac{{{V}_{2}}}{{{T}_{2}}}, which is Charles’s law.

  • It allows one to solve problems where P,V,and T are all changing.

Relationship of V and n (at constant P and T)

 Avogadro’s Law states that for a gas at constant temperature and pressure, the volume (V) is directly proportional to the number of moles of gas (n):

\frac{{{V}_{1}}}{{{n}_{1}}}=\frac{{{V}_{2}}}{{{n}_{2}}}

In other words, at the same temperature and pressure, 4 moles of a gas would take up twice the volume as 2 moles of a gas.  Or, in another example, if:

A(g) →2 B(g),

each volume of gas A that reacted would produce a volume of gas B twice that of gas A.

More information, applications, and solved examples of all these gas laws can be found in Section 9.2 of OpenStax.

Objective 3 Practice

Objective 5: Know the value of STP

When working with gas laws, you will likely encounter a set of conditions called STP, which stands for Standard Temperature and Pressure.  It is a shorthand way to define the temperature and pressure:

  • P = exactly 1 atmosphere (omit from significant figure conditions)
  • T = 0 °C = 273.15 K

When you see a gas “at STP”, you are given a temperature of 273.15 K and a pressure of 1 atm.

Objective 4: Solve problems using the ideal gas law.

The ideal gas law summarizes all of the gas laws looked at so far in one relationship:

PV=nRT

where R=0.0821\frac{L\cdot atm}{mol\cdot K}

The only parameter here that is new to you is R, the universal ideal gas constant.  Is is a proportionality constant whose numerical value depends on the units.

There are many more values of R with different combinations of units (see this link).  So which one should you use?  You choose the R with units that match your units of pressure, volume, number of mole, and temperature.

Therefore , if you wish to use R=0.0821\frac{L\cdot atm}{mol\cdot K}, use

  • volume in L
  • pressure in atm
  • n in moles
  • temperature in K

The ideal gas law PV=nRT contains all the other gas laws.  As an example, Charles’s law states that the volume of a fixed quantity (constant n) of gas at constant P is directly proportional to the  absolute (Kelvin) temperature.  If PV=nRT, then \frac{V}{T}=\frac{nR}{P}.  If n and P are constant, and R is always a constant, that means V/T does not change, so

\frac{{{V}_{1}}}{{{T}_{1}}}=\frac{{{V}_{2}}}{{{T}_{2}}}

which is Charles’s Law.

Additionally, the ideal gas law allows us to solve problems in which three of the four variables (P,V,T, and n) are given and you are asked to solve for the fourth.  A good example of this is Example 9.9 in OpenStax Section 9.2.

Finally, about the word “ideal”. It refers to a theoretical model of a gas that will be discussed soon in one of the later objectives.  This model works quite well at the temperatures and pressures we live at everyday, so assuming gases are ideal allows us to make a lot of reasonably accurate predictions.

Objective 4 example:

Calculate the volume of 1 mole of an ideal gas at STP.

You are given:

  • n=1 mol
  • T=273.15 K (from STP)
  • P=1 atm (from STP)

Using PV=nRT, you can isolate V to solve and plug in the values.  We will use the value of R containing atm, mol, and K, which is R=0.0821\frac{L\cdot atm}{mol\cdot K}

V=\frac{nRT}{P}=\frac{(1mol)\left( 0.0821\frac{L\cdot atm}{mol\cdot K} \right)(273.15K)}{1atm}=22.4L

Therefore, the volume of 1 mole of any ideal gas at STP is about 22.4 L.  This is called the standard molar volume and is often reffered to and used as a handy shortcut in problems. Standard molar volume is discussed further in OpenStax Figure 9.18).  Remember, though, that a gas only has a volume of 22.4 L/mol at STP (not at other temperatures and pressures).

This figure shows three balloons each filled with He, NH subscript 2, and O subscript 2, respectively. Beneath the first balloon is the label “4 g of He” Beneath the second balloon is the label, “17 g of NH subscript 2.” Beneath the third balloon is the label “32 g of O subscript 2.” Each balloon contains the same number of molecules of their respective gases.

Objective 4 and 5 Practice:

Objective 6: Starting with the ideal gas law, derive a relationship that includes molar mass and gas density and then solve problems using it.

The ideal gas law is PV=nRT.  We can also derive another form of the ideal gas law that includes molar mass (g/mol) and gas density (g/L) instead of volume and moles.

Beginning with the ideal gas law: PV=nRT

and recognizing that density is mass/volume: D=\frac{m}{V}

and molar mass of a gas (we will use the symbol μ for molar mass) is mass (in g) divided by moles of gas (n):\mu =\frac{mass}{n}

Rearranging the ideal gas law gives P=\frac{nRT}{V}.

Rearranging \mu =\frac{mass}{n} gives n=\frac{mass}{\mu }

Substituting \frac{mass}{\mu } for n in the rearranged ideal gas law:

P=\frac{nRT}{V}=\frac{massRT}{V\mu }

Substituting D for mass/V (since D=\frac{m}{V})

P=\frac{DRT}{\mu } or P\mu =DRT

This form of the ideal gas law relates molar mass and gas density.  Here is an example of a problem that can be solved using this relationship:

Objective 6 Example:

Calculate the density of NH3 (g) at 100 °C and 1.15 atm

P\mu =DRT can be rearranged to solve for density:

\frac{P\mu }{RT}=D

Given values include:

  • T=100 °C+273=373 K
  • P=1.15 atm
  • μ=17.0 g/mol for NH3

Plugging in the given values for T, μ and P and the gas constant R:

\frac{(1.15atm)\left( 17.0\frac{g}{mol} \right)}{\left( 0.0821\frac{L\cdot atm}{mol\cdot K} \right)(373K)}=D=0.638\frac{g}{L}

Note this problem could also be solved from the ideal gas law PV=nRT

Rearranging PV=nRT gives \frac{n}{V}=\frac{P}{RT}

\frac{n}{V}=\frac{P}{RT}=\frac{1.15atm}{\left( 0.0821\frac{L\cdot atm}{mol\cdot K} \right)(373K)}=0.03755\frac{mol}{L}

We can then go from mol/L to density via dimensional analysis:0.03755\frac{mol}{L}\times 17.0\frac{g}{mol}=0.638\frac{mol}{L}

This approach gives the same result (as it should!).  As your instructor, I don’t care what approach you use to solve these problems, I care only that you can solve them.  Use the approach that works best for you!

Note in OpenStax section 9.3 the equation is written as D=μPRT.  This is a typo and is incorrect.

Objective 6 Practice:

Objective 7: Using a balanced equation, convert from a given mass, mole, or volume of one gas phase substance to mass, mole, or volume of another.

Stoichiometry

As we saw in the first unit (and again in our previous topic of solutions), you can identify a stoichiometry problem when you are working with a known or given chemical reaction, are given information that will allow you to determine the number of moles of one of the reactants or products, and you wish to determine information about one of the other reactants or products.  All stoichiometry problems involve the same three steps:

  1. Use given information to calculate moles of a reactant or product.
  2. Use the chemical equation and mole ratio to go from the moles of a reactant or product in step one to the moles of reactant or product you are asked about
  3. From the moles of reactant or product from step 2, complete the problem by calculating the answer.

You were introduced to one type of stoichiometry problem in the last unit (in Chapter 3).  This was a mass-mass stoichiometry problem.  For those problems, the three steps were:

  1. Given grams to moles of a reactant or product
  2. Moles of a reactant or product to moles of another reactant or product using the chemical equation and mole ratio
  3. Moles from step 2 to grams

In gas stoichiometry problems, steps 1 and/or 3 can be replaced by an ideal gas law calculation, using a given P,V,and T so solve for moles or moles to calculate P,V, or T.   Try this practice problem as an example:

Objective 7 Practice:

Hydrazine (N2H4) reacts with oxygen according to the equation {{\text{N}}_{2}}{{\text{H}}_{4}}(g)\text{ }\!\!~\!\!\text{ + }\!\!~\!\!\text{ }{{\text{O}}_{2}}\text{(g) }\!\!~\!\!\text{ }\to \text{ }\!\!~\!\!\text{ }{{\text{N}}_{2}}(\text{g})\text{ }\!\!~\!\!\text{ + }\!\!~\!\!\text{ 2 }\!\!~\!\!\text{ }{{\text{H}}_{2}}\text{O(l)}

The O2 needed for the reaction is in a 450.0 L tank at 23 °C.  What must the oxygen pressure be in the tank to have sufficient oxygen to completely consume 1.00 kg of hydrazine?

See examples 9.17, 9.18, and 9.19 for additional solved examples of gas stoichiometry problems.

Objective 8: Solve problems using Dalton’s Law of Partial Pressures.

 

Dalton’s Law of Partial Pressures applies to mixtures of gases. Each gas acts as if it is the only gas in the container, and is not affected by the presence of the other gases in any way.  The total pressure is the sum of the pressures that each gas would exert if alone. 

Another name for the pressure that a gas in a mixture would exert if alone is  the partial pressure.  Therefore, in a mixture of gases the total pressure is the sum of the partial pressures.

Let’s look at an example:

Consider a sealed 10.0 L container containing a mixture of helium, oxygen, and nitrogen.  The pressure of the tank would be 2.0 atm if there were only helium, 3.0 atm if there were only oxygen, and 5.0 atm if there were only nitrogen.  What is the total pressure in the tank?

The total pressure will be the sum of the three partial pressures (of helium, oxygen, and nitrogen).

{{P}_{total}}={{P}_{He}}+{{P}_{{{O}_{2}}}}+{{P}_{{{N}_{2}}}}=2.0+3.0+5.0=10.0atm

What happens to volume when gases are mixed?

Suppose 3.0 L of helium gas at a pressure of 1.0 atm and 2.0 L of oxygen gas at a pressure of 1.0 atm were both transferred to a 10.0 L tank.  Room temperature was maintained throughout.  What would be the final gas volume?

Remember : For an ideal gases, if you put different gases in a mixture, it doesn’t change the volume- volumes of individual gas particles is not important.  All the gases will mix and take up all the space available to them in whatever container they are in.  What would happen in the example above as the partial pressures of each gas would change by Boyle’s Law as they went into the new, larger volume.

Dalton’s Law and mole fraction

The mole fraction (χ) of a gas in a mixture is defined as the moles of that gas divided by the total moles of gas in the mixture.

{{\chi }_{1}}=\frac{{{n}_{1}}}{{{n}_{total}}}=\frac{{{n}_{1}}}{{{n}_{1}}+{{n}_{2}}+n{}_{3}^{{}}+\ldots }

If we look at the Ideal Gas Law, the moles of a gas and pressure are directly proportional at constant V and T:

PV=nRT or n=\frac{PV}{RT}

Since a mixture of gases in a container will always have the same temperature and volume, the ratio of the moles of gases will always be the same as the ratio of the pressures.  In our example above:

Consider a sealed 10.0 L container containing a mixture of helium, oxygen, and nitrogen.  The pressure of the tank would be 2.0 atm if there were only helium, 3.0 atm if there were only oxygen, and 5.0 atm if there were only nitrogen. 

Helium provides 2/10 or 0.2 of the total pressure (partial pressure of He = 2.0 atm, total pressure = 10.0 atm.  Therefore, it also provides 2/10 of the total moles of gas.  In a mix of gases, the total number of moles of gas, not the identity, determine the pressure.

We can express this mathematically as:

{{\chi }_{1}}=\frac{{{n}_{1}}}{{{n}_{total}}}=\frac{{{P}_{1}}}{{{P}_{total}}}

So the mole fraction of helium would be:

{{\chi }_{He}}=\frac{{{P}_{He}}}{{{P}_{total}}}=\frac{2.0atm}{10.0atm}=0.20

Similarly, χoxygen=0.30 and χnitrogen=0.50.

Figure 9.20 in OpenStax (and examples 9.14 and 9.15 drectly below it) provide additional illustrations and examples of Dalton’s Law.

Objective 8 practice

Objective 9: Calculate the mass of a reactant given the volume, total pressure, and temperature of a gas collected over water.

Vapor Pressure:

When a closed container is partially filled with liquid, some molecules evaporate into the vapor or gas phase.  As the number of molecules in the vapor phase increase, some start to condense back into the liquid.  These molecules of vapor over a liquid in a closed container cause pressure.  Eventually, the rate of condensation is equal to the rate of evaporation and an equilibrium is reached.  The pressure of the molecules in the gas phase at equilibrium is called vapor pressure. Vapor pressure for any liquid increases as temperature increases and is known for many liquids as a function of temperature.  For example, the vapor pressure of water at various temperatures is shown in Table 9.2 in OpenStax.

An experimental technique called collection of a gas over water (illustrated in Figure 9.21 in OpenStax) is a simple way to measure the gas produced in a chemical reaction:

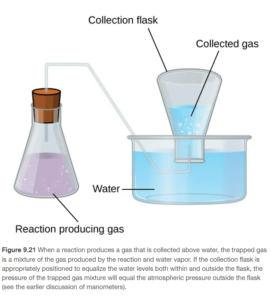
This figure shows a diagram of equipment used for collecting a gas over water. To the left is an Erlenmeyer flask. It is approximately two thirds full of a lavender colored liquid. Bubbles are evident in the liquid. The label “Reaction Producing Gas” appears below the flask. A line segment connects this label to the liquid in the flask. The flask has a stopper in it through which a single glass tube extends from the open region above the liquid in the flask up, through the stopper, to the right, then angles down into a pan that is nearly full of light blue water. This tube again extends right once it is well beneath the water’s surface. It then bends up into an inverted flask which is labeled “Collection Flask.” This collection flask is positioned with its mouth beneath the surface of the light blue water and appears approximately half full. Bubbles are evident in the water in the inverted flask. The open space above the water in the inverted flask is labeled “collected gas.”

The collection flask is partially filled with water then inverted into a dish or bowl filled with water.  The gas is then allowed to fill the area at the bottom (now top since inverted) of the flask.  The flask’s height can be adjusted so the total pressure of the gas in the flask equals the barometric pressure.  The pressure of the gas being measured can then be calculated as the difference between the total pressure and the vapor pressure of water.  An example of how this technique can be used is below:

Collection of a gas over water example problem:

When heated, potassium chlorate decomposes in the following reaction:

2\text{ }\!\!~\!\!\text{ KCl}{{\text{O}}_{3}}\text{(s)}\to 2\text{ }\!\!~\!\!\text{ KCl }\!\!~\!\!\text{ (s) }\!\!~\!\!\text{ + }\!\!~\!\!\text{ 3 }\!\!~\!\!\text{ }{{\text{O}}_{2}}(\text{g)}

If 327 mL of O2 is collected over water at 19 °C and 735 torr how many grams of potassium chlorate (KClO3) were consumed?  The vapor pressure of water at 19 °C is 16.5 torr.

The problem is solved in this video:

 

 

Objective 10: List and explain the principle points of the kinetic molecular theory of gases and describe the factors responsible for real gases deviating from ideal gases.

Objective 11: Describe the relationship between temperature, average velocity, and kinetic energy.

Objective 12:State Graham’s law and use it to solve problems.

So far, in this topic, we have looked at laws that summarize and describe the behavior of gases.  Now we will shift over and look at the theory that explains these laws.   The theory is called the kinetic-molecular theory of gases.

The Kinetic-Molecular Theory of Gases

The theory describes what gases look like on the atomic or molecular level as follows:

  • Gases consist of large numbers of atoms or molecules that are in continuous, random motion.  Individual gas particles (whether atoms or molecules) are always moving rapidly in random direction.
  • The combined volume of all the molecules of the gas is negligible compared to the volume in which the gas is contained.  This is another way of saying that a gas is mostly empty space.  We can add more gas and the volume does not change.  The particles are so far apart from eac other compared to their size that essentially each one is able to move and behave as if it is alone (do you see how that connects with Dalton’s Law?)
  • Attractive and repulsive forces between gas molecules are negligible. The particles do not collide with or affect each other in any way.
  • The average kinetic energy of the molecules is proportional to the absolute (Kelvin) temperature. This will be discussed more next, but the higher the temperature, the faster the individual particles move.
  • At any given temperature the molecules of all gases (regardless of molecule shape, size, or weight) have the same average kinetic energy. Also discussed next.

Molar Mass, Average Speed, and Average Kinetic Energy

Kinetic energy is energy of motion.  Some of you may remember from studying physics that the kinetic energy of a moving object can be calculated by:

KE=\frac{1}{2}m{{v}^{2}}

where m is mass and v is velocity (velocity is speed in a direction).  Kinetic molecular theory says:

  • The average kinetic energy of the molecules is proportional to the absolute (Kelvin) temperature.
  • At any given temperature the molecules of all gases (regardless of molecule shape, size, or weight) have the same average kinetic energy.

This means, that is the kelvin temperature of a gas doubles then the kinetic energy of the particles making up the gas doubles.  Since the mass does not change, the velocity must have increased and the molecules are moving faster.  Also, all gases, whether hydrogen, oxygen, chlorine, carbon dioxide, or anything else, have the same average kinetic energy at the same temperature.  That means, looking at the equation,

KE=\frac{1}{2}m{{v}^{2}},

heavier gases (with higher molar mass) must have lower velocity than lighter gases (with lower molar mass).

Example

Helium (molar mass or μ=4 ) is lighter than methane (CH4 :μ=16).  At the same temperature, how many times faster would a helium atom move than a methane molecule?

\frac{1}{2}{{m}_{He}}{{v}_{He}}^{2}=\frac{1}{2}{{m}_{methane}}{{v}_{methane}}^{2}

Canceling the 1/2 ‘s

{{m}_{He}}{{v}_{He}}^{2}={{m}_{methane}}{{v}_{methane}}^{2}

Rearranging

\frac{{{v}_{He}}^{2}}{{{v}_{methane}}^{2}}=\frac{{{m}_{methane}}}{{{m}_{He}}}

taking the square root of both sides and plugging in the masses of the atoms and molecules,

\frac{{{v}_{He}}^{{}}}{{{v}_{methane}}^{{}}}=\sqrt{\frac{{{m}_{methane}}}{{{m}_{He}}}}=\sqrt{\frac{16amu}{4amu}}=2

The ratio of two means that helium (which is 4 times lighter) must move 2 times faster to have the same kinetic energy.

Molecular Diffusion and Effusion and Graham’s law

The process of a collection of molecules spreading out from high concentration to low concentration is called diffusion.  We are often interested in diffusion, and its rate depends on many factors, we do know that lighter gases will diffuse faster than heavier gases, because the lighter gas particles move faster.

The process by which a collection of molecules escapes through a small hole into a vacuum is called effusion.  As is the case with diffusion,  lighter gas will effuse more rapidly than a heavy gas.  However, because of its controlled environment and nature (no wind currents, concentration gradients, or other factors), effusion is much easier to study, and relative rates of effusion for different gases is the same as their relative rates of diffusion. Graham studied effusion with various gases and Graham’s law is a result of that study.

Graham’s Law of Effusion

Graham’s law states that the rate of effusion of a gas is inversely proportional to the square root of its molar mass.  This directly results from all gases having the same average kinetic energy at the same temperature.

\frac{\text{rat}{{\text{e}}_{\text{gas }\!\!~\!\!\text{ 1}}}}{\text{rat}{{\text{e}}_{\text{gas }\!\!~\!\!\text{ 2}}}}=\sqrt{\frac{{{\mu }_{\text{gas }\!\!~\!\!\text{ 2}}}}{{{\mu }_{\text{gas }\!\!~\!\!\text{ 1}}}}}

Compare this equation to the helium and methane relative velocity example above and see how the equations are the same.

Given any three of the variables above (or a ratio of the effusion rates), you should be able to solve for the unknown variable.  Examples 9.20, 9.21, and 9.22 in OpenStax Section 9.4 illustrate this.

Objective 10-12 Practice

Objective 13: Explain the origin of the correction terms to P and V that appear in the Van der Waal’s equation.

Deviations from ideal gas behavior

If you look back above at the Kinetic Molecular Theory and its description of gases, you can see that it makes two assumptions for gases that are not quite true – they are idealizations, which is where the name “ideal gas” comes from.  These assumptions are:

  • The individual gas particles have zero volume
  • There are no interactions between the particles and they or any collisions do not affect each other in any way

Even though no gas is truly ideal, these assumptions are close to true for the temperatures and pressures that we live at and most often work with – around room temperature and pressure of around 1 atm or less.  Therefore, the ideal gas laws work quite well at those temperatures and pressures, which is why we use them so much.

At higher pressures and at very low temperatures, though, gases deviate more from ideal behavior and the ideal gas law doesn’t work do well anymore — giving predictions that do not match up with what is observed experimentally.  In these conditions, gases are called “real gases“.

Deviations are more pronounced in high molar mass gases than in low molar mass gases, since larger molecules take up more volume.  For this region, a gas like chlorine with a higher molar mass would begin to deviate significantly from the ideal gas law at a higher temperature and lower pressure than a gas with a lower molar mass like helium.

Van der Waal’s Equation

Van der Waal’s equation(see below) is similar to as law, but includes corrections introduced by van der Waal for volume (subtracting nb) and pressure (adding \frac{{{n}^{2}}a}{{{V}^{2}}}). It is used for real gases, which are gases that do not follow the predictions of the ideal gas law (deviations from the ideal gas law occur at low temperature and high pressure.

\left( P+\frac{{{n}^{2}}a}{{{V}^{2}}} \right)\left( V-nb \right)=nRT

The constants a and b are called van der Waal constants and have different values for different gaseous elements and compounds.  There values have been determined by experiment – that is, real gases temperature, pressure, and volumes have been measured under a variety of conditions until the a and b values that make the equation work were determined.Table 9.3in OpenStax lists the values for some gases.

You will not solve numerical problems with the van der Waal equation in this class, but you should understand the general equation,  corrections to temperature and pressure and why it is employed.

A more detailed explanation of the equation and corrections is available in OpenStax Section 9.6.

 

Objective 13 Practice

css.php