Nuclear Chemistry

Nuclear chemistry is the study of nuclear reactions and their uses. Up to this point in your study of chemistry, there has been a large focus on the electrons when looking at atoms and molecules. Electrons largely determine an element’s behavior in chemical change or chemical reactions. In this topic, we will shift our focus to the nucleus and nuclear reactions.

Just as we have used chemical formulas and chemical reactions to discuss chemical substances and chemical change, in nuclear chemistry we use nuclear symbols and nuclear reactions. You have likely seen nuclear symbols before but nuclear equations are more likely to be new to you. They are both discussed next.

Nuclear symbols

Whether you took CHEM 151 at LCC or a first semester course elsewhere, you have likely seen nuclear symbols (it not, that’s OK, we’ll review). A brief review follows here, but if you would like a more detailed review of nuclear symbols and isotopes, you can see Objectives 4 and 5 in my CHEM 151 notes on Atoms, Molecules, and Ions and OpenStax Table 2.4.

The following is a nuclear symbol for carbon-14:

${}_{6}^{14}C$

In this symbol:

The upper left number (14) is the mass number (A). It is the total number of protons and neutrons in the nucleus.
The lower left number (6) is the atomic number (Z). It is the total number of protons in the nucleus. It determines the element (carbon – C – in this example).

Since the element symbol determines the atomic number and vice versa, it is sometimes omitted, so ${}_{6}^{14}C$ can be shown as ${}_{{}}^{14}C$ , C-14, or carbon-14.

Nucleons are the protons or neutrons making up the nucleus of the atom. Carbon-14 has 14 nucleons – 6 of them are protons and 8 are neutrons.

Example

Isotopes

Isotopes are atoms of the same element with different number of neutrons. They have the same atomic number but different mass numbers. Different isotopes of the same element are distinguished by their mass numbers. Different isotopes of an element are chemically almost identical, but may have different behaviors in nuclear reactions. A nuclide is a class of nuclei with the same number of protons and neutrons.

Nuclear Equations

Nuclear symbols (including atomic and mass numbers) represent the reactant and product nuclei. In nuclear equations, is is assumed that the products and reactants are nuclei (atoms without electrons). Here is an example of a balanced nuclear equation:

${}_{92}^{238}U\to {}_{2}^{4}He+{}_{90}^{234}Th$

As you can see, balancing nuclear equations is very different than balancing chemical equations. In balanced nuclear equations, the totals of the mass numbers on both sides of the equation are equal and the totals of the atomic numbers on both sides are equal. The total of the top (mass) numbers is 238 on both sides. The total of the bottom (atomic) numbers is 92 on both sides.

Note the identities of the elements can change. As we will see, sometimes balanced nuclear equations will also include coefficients.

If you are given all but one of the products or reactants in a nuclear equation, you should be able to deduce the remaining one by balancing and difference. An example is shown in OpenStax Section 21.2 (Example 21.4)

Objective 1: Define and apply the definition for radioactive decay.

When nuclei change spontaneously they are said to be radioactive, and they undergo radioactive decay. This occurs when nucleus has an unstable neutron to proton ratio.

Unstable nuclides will decay, losing particles in an attempt to move toward a more stable neutron to proton ratio. A radionuclide is a radioactive nucleus. Isotopes that are radioactive are called radioisotopes.

Example

${}_{92}^{238}U\to {}_{2}^{4}He+{}_{90}^{234}Th$

The radionuclide uranium-238 undergoes radioactive decay. Over time, a population of uranium will spontaneously lose a particle consisting of two protons and two neutrons (as we will see soon, this is known as an alpha particle and is equivalent to a helium nucleus), resulting in thorium -234.

Objective 2: Classify the types of radioactive decay processes and describe the characteristic of each.

Objective 3: Write the nuclear symbol for protons, neutrons, electrons, alpha particles, beta particles and positrons.

Objective 4: Write balanced nuclear equations for radioactive decay processes or nuclear transmutations.

Radioactive isotopes can decay by several processes. The processes or types of radioactive decay include alpha emission, beta emission, positron emission, gamma radiation, and electron capture.

These types of decay are discussed in detail in OpenStax Section 21.3. Figure 21.7 in that section provides a nice summary and overview of the types of decay.

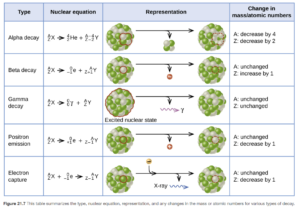
Alpha Emission (α)

In alpha (α) emission or alpha decay, the nucleus emits an α particle, which is a helium nucleus (helium atom without electrons). While alpha particles are the largest radioactive decay particles, they are the least effective at penetrating matter. They can be stopped by paper.

It is a common mode of decay for heavy nuclides in the lower rows of the periodic table (atomic number of >83). Light isotopes in the first few rows of the periodic table generally do not exhibit alpha decay.

The nuclear symbol for an alpha particle is ${}_{2}^{4}He\text{ }\!\!~\!\!\text{ or }\!\!~\!\!\text{ }{}_{2}^{4}\alpha$

Example

Write the equation for alpha decay of uranium-238

It is shown in the video below:

Beta Emission (β)

During beta emission or beta decay, a neutron in the nucleus is converted to a proton. The released energy results in formation of an electron. These high-speed electrons are called beta (β) particles. They are emitted from the nucleus and are not one of the electrons from the atom the nucleus is in. They are smaller but penetrate matter more readily than alpha particles They are stopped by sheets of aluminum or other metals.

The nuclear symbol for a beta particle is

${}_{-1}^{0}e\text{ }\!\!~\!\!\text{ or }\!\!~\!\!\text{ }{}_{-1}^{0}\beta$

Example

Write an equation for the beta decay of thorium-234

The symbol for thorium-234 is ${}_{90}^{234}Th$ . The atomic number of 90 is obtained from the periodic table. Since thorium is undergoing beta decay, it will be the reactant and the beta particle will be the product:

${}_{90}^{234}Th\to {}_{-1}^{0}e+\_\_\_$

To fill in the blank, balance the atomic and mass numbers:

${}_{90}^{234}Th\to {}_{-1}^{0}e+{}_{91}^{234}Pa$

Note the mass number of the daughter (product) nuclide is 91, as 91 +-1 = 90 is needed to balance. Pa (protactinum) is element 91.

Gamma Radiation (γ)

Gamma radiation is made up of high energy photons released by a nucleus with excess energy . It often accompanies α or β decay. Gamma particles are the smallest but most penetrating radioactive particles (blocked by lead). They cause radiation damage when they ionize matter.

The nuclear symbol for a gamma particle is

${}_{0}^{0}\gamma$

Example

${}_{92}^{238}U\to {}_{2}^{4}He+{}_{90}^{234}Th+{}_{0}^{0}\gamma$

You will not be expected to predict whether gamma radiation will occur in a reaction, but you should be able to identify it as a “fill in the blank” on a reaction.

Positron Emission (β)

During positron emission, the nucleus emits a positron. A positron is a particle with the same mass as an electron but with the opposite sign. With positron emission, a proton in the nucleus is converted to a neutron.

The nuclear symbol for a positron is ${}_{1}^{0}e$

Example

The positron emission of Na-22 can be written as:

${}_{11}^{22}Na\to {}_{1}^{0}e+{}_{10}^{22}Ne$

Electron Capture

The nucleus captures an electron from the electron cloud surrounding the nucleus. It results in proton to neutron conversion. It differs from the other decay processes (which are all emissions, where the particle is a product). With electron capture, the captured electron is on the reactant side.

Example

${}_{80}^{201}Hg+{}_{-1}^{0}e\to {}_{79}^{201}Au+{}_{0}^{0}\gamma$

Note there is also a gamma emission accompanying this alpha emission, but this is not always the case.

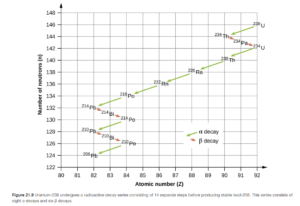
Radioactive Series

Large radioactive nuclei do not stabilize by undergoing only one radioactive decay. They undergo a series of decays until they form a stable nuclide. You may have noticed that the thorium-234 product of the alpha decay example was the reactant in the beta decay example. These are the first two steps in the uranium-238 decay series. The entire series (ending with Pb-206), is shown in OpenStax Figure 21.9.

Objective 2-4 Practice

Answer the questions for the following processes:

${}_{79}^{201}Au$ undergoes electron capture

Positron emission by ${}_{54}^{131}Xe$

${}_{53}^{128}I$ produces a beta particle

Alpha decay by Pu-240

Objective 5: Complete and balance nuclear reactions given all but one of the particles involved.

Additional particles that are common in radioactive decay and nuclear transformation reactions include:

neutron: ${}_{0}^{1}n$

proton: ${}_{1}^{1}p\text{ }\!\!~\!\!\text{ or }\!\!~\!\!\text{ }{}_{1}^{1}H$

Knowing these particles, and the ones discussed previously, you should be able to complete and balance nuclear reactions given all but one of the particles involved.

Figure 21.4 in OpenStax offers a nice listing of all the common particles in nuclear reactions in a tabular form.

Objective 5 Practice

${}_{67}^{164}Ho+{}_{-1}^{0}e\to \_\_\_\_\_$

${}_{95}^{241}Am+\_\_\_\_\_\to {}_{97}^{243}Bk+2{}_{0}^{1}n$

${}_{9}^{17}F\to {}_{8}^{17}O+\_\_\_\_\_$

${}_{51}^{129}Sb\to {}_{-1}^{0}e+\_\_\_\_\_$

Objective 6: Describe the role that the neutron-to-proton ratio, magic numbers, and odd-even number (protons & neutrons) play in accounting for the stability of a nucleus.

Objective 7: Predict whether a nuclide is likely to be stable or unstable (radioactive). If unstable, predict the most likely mode of decay to achieve stability. (For example, explain why tritium, ³H, is unstable.)

The Belt of Stability and neutron to proton ratio

The belt of stability (also called band of stability) is the portion of a graph of number of protons vs. number of neutrons that contains all stable nuclei. The majority of the radioactive nuclides occur outside this belt. Again, stable means a nuclide will not undergo radioactive decay; radioactive means that it will.

Click this link to see the belt of stability and look at it as you read the following sentences.

What governs stability is the ratio of neutrons to protons (n/p ratio). It would be nice if there were one stable n/p ratio that applied to all nuclides, unfortunately reality is more complicated.

For smaller nuclides (up to around an atomic number of 20) a neutron/proton ratio of approximately 1 is stable. Beyond Z=20, the necessary n/p ratio for stability begins to gradually increase, up to about 1.6 by the time an atomic number of around 80 is achieved. This gradual increase of stable n/p ratio is shown by the blue line on the belt of stability. All nuclides with atomic numbers>83 are unstable (radioactive). They tend to undergo alpha emission but can undergo others.

Neutron to proton ratio and types of decay (belt of stability effect)

We would expect nuclides with high n/p ratios to produce β particles, since beta decay converts a neutron to a proton. Let’s look at an example:

$\begin{array}{*{35}{l}} ~ \\ {}_{6}^{14}C~\to {}_{-1}^{0}e+\text{ }{}_{7}^{14}N \\ \end{array}$

Carbon-14 is a beta emitter. It has 8 neutrons and 6 protons, giving a n/p ratio of 1.33. After the beta emission, the daughter nuclide nitrogen-14 has 7 neutrons and 7 protons (see how a neutron was converted to a proton), a n/p ratio of 1.

For similar (but opposite) reasons, both positron emission and electron capture increase n/p ratio, as they result in the conversion of a proton to a neutron. We would therefore expect those types of decay when the n/p ratio is too low or below the belt of stability.

More Trends in Nuclear Stability

Nuclei with certain numbers of protons or neutrons are generally more stable than nuclei with other numbers. These numbers: 2,8,20,28,50 or 82 protons or 2,8,20,28,50,82 or 126 neutrons are known as “magic numbers”. Although we will not go into it in this introductory level, this is a consequence of the quantum mechanics of the nucleus (similar to the idea of noble gas electron configurations or filled electron shells being stable).

Nuclei with an even number of both protons and neutrons are generally more stable than those with odd number of neutrons. This is illustrated in Table 21.1 of OpenStax.

Objective 6 and 7 Practice

Objective 8: Calculate the half-life of a radioactive nuclide given the rate constant or vice-versa.

Objective 9: Given any two of the following variables involved in the rate of radioactive decay, calculate the third. Variables: 1) Amount of sample, 2) Activity, 3) Decay constant, 4) Half-life, 5) Time.

Kinetics of Radioactive Decay

Radioactive decay processes can be thought of as A→products reactions just like the ones we dealt with in chemical kinetics. They follow first order rate laws, so the first order rate laws and integrated rate laws you studied in chemical kinetics apply. The only difference is that rather than concentration of reactant ([A]) we deal with population of radioactive nuclides (N).

For radioactive decay, The rate law is $rate\text{ }\!\!~\!\!\text{ }=\text{ }\!\!~\!\!\text{ }kN$

The integrated rate law is:

$\ln N=-kt+\ln {{N}_{0}}$

where

k is the rate constant
t is time
N is the population of radionuclides at time t
N₀ is the population of radionuclides at time=0 (the initial population)

Given any three of the quantities, you should be able to solve for the fourth.

The first order rate law is often shown in two other ways (which are just different forms of the same equation above). You can use any of the three forms

$\ln \frac{N}{{{N}_{0}}}=-kt$

$\ln \frac{{{N}_{0}}}{N}=kt$

Hopefully, these equations look familiar to you as they are the same as the first order rate law and integrated rate law equations for chemical kinetics (with N replacing [A]).

One other piece: in chemical kinetics, half lives are most often measured in seconds or minutes, so reasonable values of rate constants are expressed in s^-1or min^-1. But half lives of radioisotopes vary widely, ranging from a few microseconds to millions of years. Accordingly, you might encounter rate constants in units of s^-1, day^-1, or year^-1.

Try the example problems below; your strategies should be similar to the ones used to solve chemical kinetics first order problems.

Objective 8 and 9 Practice

Objective 4: Write balanced nuclear equations for radioactive decay processes or nuclear transmutations.

Objective 5: Complete and balance nuclear reactions given all but one of the particles involved.

Nuclear Transmutations

Nuclear transmutations are processes where one nuclide is converted to another. One way transmutations occur is via radioactive decay. Another way is via nuclear reactions resulting from collisions between nuclei or between a nucleus and a neutron. Equations for these reactions are balanced the same way as radioactive decay reactions.

Example of a nuclear transmutation using high-velocity α-particles (alpha bombardment):

${}_{7}^{14}N+{}_{2}^{4}He\to {}_{8}^{17}O+{}_{1}^{1}H$

In the above example, a He-4 nucleus (alpha particle) collides with a N-14 nucleus. This is called alpha bombardment of N-14 as the nitrogen nuclei are bombarded with alpha particles. For this transmutation to occur, the He-4 and N-14 nuclei (not atoms) actually have to collide. This is difficult because nuclei are positively charged and repel each other. These nuclei have to be accelerated to a very high velocity to overcome the repulsion and collide. Particle accelerators such as cyclotrons are used to accelerate particles using strong magnetic and electrostatic fields. This website from CERN describes how particle accelerators (includes pictures and videos). You can also see more detail and description on accelerators in OpenStax section 21.4.

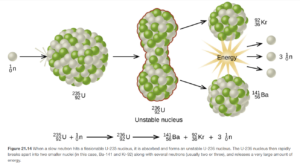
Neutron Bombardment

Since neutrons have no charge, they do not have to be accelerated to high velocities like positive particles (alpha, other nuclei, etc) to cause nuclear reactions. Neutron bombardment is used in fission reactors in nuclear power plants. Examples of fission reactions resulting from neutron bombardment is shown in Figure 21.14 (and Figure 21.15 directly below it) in OpenStax.

Most synthetic isotopes used in medicine and research (for example, Co-60 for cancer therapy) are also made using neutron bombardment.

Transuranium elements

The nucleus with the highest atomic number that has been discovered as naturally occurring is uranium (Z=92). All elements with larger atomic numbers are known as transuranium elements, and are produced artificially by bombarding smaller nuclei or particles.

They can be produced by artificial means including neutron bombardment, alpha bombardment, and nuclear bombardment (bombardment of one nucleus with another).

Examples (do not memorize, but understand)

${}_{92}^{238}U+{}_{0}^{1}n\to {}_{93}^{239}Np+{}_{-1}^{0}e$

${}_{94}^{239}Pu+{}_{2}^{4}He\to {}_{96}^{242}Cm$

${}_{83}^{209}Bi+{}_{28}^{64}Ni\to {}_{111}^{272}Rg+{}_{0}^{1}n$

Note all three of these involve bombardment to produce a nuclide with an atomic number >92. The first is neutron bombardment, the second is alpha bombardment, and the third is nuclear bombardment.

More transuranium elements, and the means by which they are prepared, are shown in Table 21.3 in OpenStax.

Objective 12: Describe how radioactivity of radioactive substances is detected using a badge dosimeter, Geiger counter, and scintillation counter, radiotracers.

Radiation from radioactive decay can be detected by several means, all of which use a response of matter to radiation to detect (and in some cases quantify) levels of radiation. Somme common ones are listed and briefly discussed below.

Badge dosimeter

A badge dosimeter consists of photographic film held in a small case and pinned to clothing. The radiation exposure is determined from the extent of fogging in the dosimeter. They are used for people working with or near radioactive substances.

Geiger counter

A Geiger counter uses the property of radioactivity that it tends to produce ions in matter. In the Geiger counter, argon gas is housed in a tube. Radiation ionizes the argon gas. The ions will a flow of electrical current. The response is proportional — the more radiation, the more ions, and the greater the current. The current is measured, thereby providing a measurement of radiation.

Scintillation counter

A substance called a phosphor is allowed to interact with radiation. Light is produced when radiation strikes the phosphor. This light is detected and used to quantify the amount of radiation.

Radiotracers

Used to measure the speed of chemical processes and to follow an element through a chemical reaction. If a radioactive isotope is included with the bulk chemical element in reactants and products in chemical reactions, that isotope can be measured to track the reaction. As an example, C-14, a radioactive isotope of carbon, can be used to track carbon in chemical reactions.

Objective 10: State the basic assumptions made when using radiometric dating to determine the age of objects.

Objective 11: Calculate and predict the potential age of an object based on levels of concentration or C-14 within that sample or based on the given isotope ratio.

Since radioactive decay processes are first order, and since Geiger counters or other detectors can be used to detect levels of radiation, detected radiation levels along with the first order integrated rate law can be used to determine the age of objects containing even very low levels of a radioactive isotope. Radiometric dating is the method of determining the age of objects based on their isotopes and isotope abundances.

Multiple isotopes are used in radiometric dating methods, used, but the most familiar is carbon-14 dating (radiocarbon dating). Carbon-14 dating is used to determine the ages of materials of organic origin (living materials). Organic (largely carbon-based) materials carry a small amount of radioactive carbon-14 since, although the vast majority of carbon atoms are carbon-12, there is a very small, naturally occurring fraction of carbon-14. The ratio of carbon-14 to carbon-12 ratio stays constant in living things. The reason is this:

Although carbon-14 is a β emitter with a half life of 5730 years, the carbon-14 supply is replenished by neutron bombardment (from cosmic rays) of nitrogen-14:

${}_{7}^{14}N+{}_{0}^{1}n\to {}_{6}^{14}C+{}_{1}^{1}H$

So as long as the living being is exchanging carbon with the atmosphere (through breathing or photosynthesis), the C-14/C-12 ratio in the body or plant stays constant. At death, carbon-14 decays and is not replenished, and the ratio drops, resulting in ever-decreasing population of C-14 and lower counts from a Geiger counter. By measuring the ratio and comparing it to that of the atmosphere, one can estimate the age of an organic material.

What assumption is made to use first order kinetics of carbon-14 decay for carbon dating?

We use todays carbon-14 level for N₀ in the integrated rate law — however the C-14/C-12 level has not always been constant going back many thousands of years. Also, it becomes difficult to measure C-14 after nearly 10 half lives. Therefore, C-14 dating is only reliable going back around 50,000 years.

Objective 11 Example

A wooden artifact shows a decay rate of 4.50 counts/ min·g carbon. Living materials show a decay rate of 13.6 counts/ min·g carbon. What is the age of the artifact? The half life of C-14 is 5730 yrs.

Counts from a Geiger counter (can be expressed as counts/ min·g carbon) are proportional to population. Therefore the ratios of counts to initial counts will equal the ratio of population to initial population:

$\frac{{{C}_{0}}}{C}=\frac{{{N}_{0}}}{N}$

and using the integrated rate law:

$\ln \left( \frac{{{N}_{0}}}{N} \right)=\ln \left( \frac{{{C}_{0}}}{C} \right)=kt$

The problem gives C and C₀ and asks to solve for t. The value of the rate constant k can be calculated from the half life:

$\frac{\ln 2}{{{t}_{1/2}}}=k=\frac{\ln 2}{5730yr}=1.21\times {{10}^{-4}}y{{r}^{-1}}$

Plugging into the integrated rate law:

$\ln \left( \frac{{{C}_{0}}}{C} \right)=kt$

$\frac{\ln \left( \frac{{{C}_{0}}}{C} \right)}{k}=t=\frac{\ln \left( \frac{13.6}{4.5} \right)}{1.21\times {{10}^{-4}}y{{r}^{-1}}}=9100yr$

Objective 11 Practice

Objective 13: Calculate the energy or mass change in a nuclear reaction, given one of these quantities.

Nuclear reactions are known for involving very large amounts of energy. Nuclear power plants can provide a very large amount of energy from a relatively small amount of fuel. Nuclear weapons are much more destructive than conventional weapons, which are based on combustion reactions. We will next look at energy considerations in nuclear reactions and discover how we can calculate energies involved in nuclear reactions.

Energy Change in Nuclear Reactions

Energy and mass are related as a consequence of Einstein’s theory of relativity. This relationship is shown by Einstein’s famous equation:

$E=m{{c}^{2}}$

where

E is energy
m is mass
c is the speed of electromagnetic radiation (3.00X10⁸ m/s)

Since $E=m{{c}^{2}}$ , for any change in energy $\Delta E=\Delta m{{c}^{2}}$

When a system gains or loses energy, this means it gains or loses mass (since c is a constant, any change in energy is due to a change in mass.

At this point, you may well be thinking, “but what about the Law of Conservation of Mass?”. Matter cannot be created or destroyed, so the mass cannot change in the reaction.

It turns out that it does. In chemical reactions (even explosions of dynamite, TNT, and the like), the energy changes are still small enough that the mass change is too small to detect.That is why we have the Law of Conservation of Mass, and why it still works well in chemistry.

However, the mass changes in nuclear reactions are significant. The energy change in nuclear reactions is due to the gain or loss of mass in the reaction. If mass changes by Δm, then there is an associated energy change ΔE = Δmc², where c = 3.0 x10⁸ m/s is the speed of light (in a vacuum). These small, measurable changes in mass cause large changes in energy.

When using the equation Since $E=m{{c}^{2}}$ , for any change in energy $\Delta E=\Delta m{{c}^{2}}$ , it is best to use SI units with:

Δm in kg – not in grams
c = 3.00 X 10⁸ m/s

This results in an E in J since $1J=1\frac{kg\cdot {{m}^{2}}}{{{s}^{2}}}$

Let’s take a look at the energy change associated with an alpha emission.

Objective 13 Example

${}_{92}^{238}U\to {}_{2}^{4}He+{}_{90}^{234}Th$

Mass U-238 nucleus = 238.0003 amu

Mass He-4 nucleus = 4.0015 amu

Mass Th-234 nucleus = 233.9942 amu

Mass change(Δm) = ∑mass of the products – ∑mass of reactants. These masses are the masses of the nuclei, not the atoms.

The mass change per mole of uranium can be calculated as:

Δm = (4.0015 g + 233.9942 g )– 238.0003 g = -0.0046 g

Since the mass per one mole of each nuclide is the same number in grams as the mass of 1 nucleus is in amu

The energy change associated per mole with this reaction is:

$\Delta E=\Delta m{{c}^{2}}=(-0.0046g)\left( \frac{1kg}{1000g} \right){{\left( 3.00X{{10}^{8}}\frac{m}{s} \right)}^{2}}=-4.1X{{10}^{11}}\frac{kg\cdot {{m}^{2}}}{{{s}^{2}}}=-4.1X{{10}^{11}}J$

How would this calculation be different if it was per uranium nucleus instead of per mole?

The change in mass would be the same, but in amu ; -0.0046 amu

$\Delta E=\Delta m{{c}^{2}}=(-0.0046amu)\left( \frac{1g}{6.022\times {{10}^{23}}amu} \right)\left( \frac{1kg}{1000g} \right){{\left( 3.00X{{10}^{8}}\frac{m}{s} \right)}^{2}}=-6.8X{{10}^{-13}}\frac{kg\cdot {{m}^{2}}}{{{s}^{2}}}=-6.8X{{10}^{-13}}J$

Objective 13 Practice

How much energy is lost or gained in the following nuclear reaction per Co-60 nucleus?

${}_{27}^{60}Co\to {}_{28}^{60}Ni+{}_{-1}^{0}e$

Mass of Co-60 atom = 59.933819 amu

Mass of Ni-60 atom = 59.930788 amu

Mass of electron = 0.000549 amu

Hint: Note mass of atoms, not nuclei are given, To calculate the masses of the cobalt and nickel nuclei, tou have to subtract the mass of each atom’s electrons from the atoms mass. Example:

mass Co-60 nucleus = mass Co-60 atom – 27(mass electron).

Find the mass of Co-60 nucleus and Ni-60 nucleus first to calculate Δm.

Objective 14: Calculate the mass defect, total nuclear binding energy, and binding energy per nucleon for a nuclide given its nuclear or atomic mass and the masses for protons, electrons and neutrons.

Mass Defect and Binding Energy

The masses of protons, neutrons, electrons, and many atoms are well known through the use of instrumentation and well-replicated measurements. So one would think that of one added up the known mass of the protons, neutrons, and electrons in an atom, the result would match up with the known mass of an atom. But it does not. An atom has a lower mass than the total mass of its protons, neutrons, and electrons. This is known as the mass defect. The nucleus has been found to be where the defect lies, so we can also sat that the mass defect is the difference between the mass of the nucleus and the total mass of the nucleons (protons and neutrons) making up the nucleus. Mass is lost (and energy released) in process of nucleons coming together to form nuclei. This energy released is called the nuclear binding energy or just the binding energy. We can also think of the binding energy as the energy required to separate a nucleus into its nucleons.

The binding energy is related to the mass defect by the same equation that relates all nuclear reaction mass changes to energy:

$\Delta E=\Delta m{{c}^{2}}$

Binding energy is typically calculated in as energy/nucleon (recall a nucleon is a proton or neutron). You may see binding energies in megaelectron volts/nucleon (MeV/nucleon) or J/nucleon. We will calculate them in J/nucleon.

See OpenStax Section 21.1 for more information on binding energy and example calculations.

Objective 14 example:

Calculate the binding energy in J / nucleon for the Fe-56 nucleus.

Mass of Fe-56 nucleus = 55.92068 amu.
Mass of a proton = 1.00728 amu
Mass of a neutron = 1.00866 amu.

Binding energy is the energy required to separate a nucleus into its protons and neutrons. Fe-36 has 26 protons and 56 neutrons, so we can write a nuclear equation illustrating this:

$26{}_{1}^{1}p$

The mass change for this reaction is the mass defect:

$\Delta m=26(1.00728)+30(1.00866)-55.92068=0.52840\text{ amu}$

From there, we can calculate the binding energy of the nucleus:

$\Delta E=\Delta m{{c}^{2}}=\left( 0.52840\text{ amu}\times \frac{1\text{ }g}{6.022\times {{10}^{23}}\text{ amu}}\times \frac{\text{1 kg}}{\text{1000 g}} \right){{\left( 3.00\times {{10}^{8}}\text{ }\frac{m}{s} \right)}^{2}}=7.90\times {{10}^{-11}}\text{ J}$

Binding energy is typically quoted in J/nucleon

$\frac{7.90\times {{10}^{-11}}\text{ J}}{56\text{ nucleons}}=1.41\times {{10}^{-12}}\frac{J}{nucleon}$

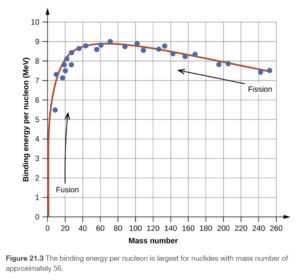
Binding Energy Curve

It turns out that Fe-56 has the highest binding energy in J/nucleon of any known nuclide. A plot of binding energy as a function of nucleons is shown on OpenStax Figure 21.3. This figure is in MeV per nucleon but it would have the same shape in J/nucleon. The higher the binding energy, the more energetically stable the nucleus. Nuclear reactions that go from species of lower binding energy to higher binding energy release energy, which is why the nuclear fission and fusion reactions discussed next release energy.

Objective 15: Distinguish between fission and fusion and state what type of nuclei will undergo these processes.

Objective 16: Based on the plot of binding energy/nucleon versus mass number, predict whether isotopes would react via fusion or fission reactions.

Binding energy for various nuclides and its role in nuclear reactions

Fission and fusion reactions both generally release energy due to the nuclides involved and their position on the binding energy curve (OpenStax Figure 21.3).

Open the link to the binding energy curve and review the following statements:

The nuclei of the light elements are generally less stable (have lower binding energy) than the heavier nuclei up to those with a mass number around 56.
The average binding energy per nucleon increases to a maximum at a mass number of 50 to 60 and decreases slowly thereafter
The nuclei around iron-56 are the most stable
Nuclides higher on the binding energy curve are more stable
Energy is released by processes moving from less stable toward more stable nuclei
These processes involve large amounts of energy since binding energy is large
Fission and Fusion are 2 ways this can occur (and we will discuss those next)

Objective 17: Identify and balance nuclear equations for fission and fusion reactions.

Some typical fission reactions are shown in Figure 21.14 and Figure 21.15 in OpenStax. In all of them, a large nuclide far on the right of the binding energy curve (keep the binding energy curve open so you can see it) is bombarded by neutrons and split into two smaller nuclides, more toward the middle of the curve (closer to Fe-56). This releases energy.

Looking at the reactions in the figures, you see that fission is often accompanied by the release of more neutrons. Neutrons produced from fission can induce another fission reaction. Eventually, a chain reaction can occur. The minimum mass of fissionable material (generally U-235) is required for a chain reaction is called the critical mass. If the mass is lower than the critical mass (subcritical mass) the neutrons escape and a chain reaction does not occur. At the critical mass one neutron from each fission is effective in causing another fission. U-235 based fission is used in nuclear weapons and nuclear power plants.

Some typical fusion reactions are shown near the bottom of the same section in OpenStax. An example is

${}_{1}^{2}H+{}_{1}^{3}H\to {}_{2}^{4}He+{}_{0}^{1}n$

Fusion occurs with very small nuclides (typically hydrogen and helium) fusing together to form something larger. Fusion can release a great deal more energy than fusion because the binding energy curve is much steeper on the left side.

Objective 18: Briefly describe the general design of a nuclear reactor.

Objective 19: State the purpose of the fuel rods, control rods, moderator and cooling fluid in nuclear reactors.

Objective 20: Identify the advantages of a fusion reactor over a fission reactor and explain the problems with using nuclear reactors as energy sources.

Nuclear reactors

Read over the section “nuclear reactors” in Chap 21 of the Brown and LeMay text (link from MyLabsPlus) or the section titled Nuclear Fission (around Figure 21.14in OpenStax).

Be able to answer questions including:
Describe the general design of a nuclear reactor (Objective 18)
State the purpose of the fuel rods, control rods, moderator, and cooling fluid in a nuclear reactor (Objective 19)
Identify the advantages of a fusion reactor over a fission reactor and explain the problems with using the nuclear reactors as energy sources (Objective 20)

Nuclear Chemistry

Nuclear symbols

Example

Isotopes

Nuclear Equations

Objective 1: Define and apply the definition for radioactive decay.

Example

Objective 2: Classify the types of radioactive decay processes and describe the characteristic of each.

Objective 3: Write the nuclear symbol for protons, neutrons, electrons, alpha particles, beta particles and positrons.

Objective 4: Write balanced nuclear equations for radioactive decay processes or nuclear transmutations.

Alpha Emission (α)

Example

Beta Emission (β)

Example

Gamma Radiation (γ)

Example

Positron Emission (β)

Example

Electron Capture

Example

Radioactive Series

Objective 2-4 Practice

Objective 5: Complete and balance nuclear reactions given all but one of the particles involved.

Objective 5 Practice

Objective 6: Describe the role that the neutron-to-proton ratio, magic numbers, and odd-even number (protons & neutrons) play in accounting for the stability of a nucleus.

Objective 7: Predict whether a nuclide is likely to be stable or unstable (radioactive). If unstable, predict the most likely mode of decay to achieve stability. (For example, explain why tritium, 3H, is unstable.)

The Belt of Stability and neutron to proton ratio

Neutron to proton ratio and types of decay (belt of stability effect)

More Trends in Nuclear Stability

Objective 6 and 7 Practice

Objective 8: Calculate the half-life of a radioactive nuclide given the rate constant or vice-versa.

Objective 9: Given any two of the following variables involved in the rate of radioactive decay, calculate the third. Variables: 1) Amount of sample, 2) Activity, 3) Decay constant, 4) Half-life, 5) Time.

Kinetics of Radioactive Decay

Objective 8 and 9 Practice

Objective 4: Write balanced nuclear equations for radioactive decay processes or nuclear transmutations.

Objective 5: Complete and balance nuclear reactions given all but one of the particles involved.

Nuclear Transmutations

Example of a nuclear transmutation using high-velocity α-particles (alpha bombardment):

Neutron Bombardment

Transuranium elements

Examples (do not memorize, but understand)

Objective 12: Describe how radioactivity of radioactive substances is detected using a badge dosimeter, Geiger counter, and scintillation counter, radiotracers.

Badge dosimeter

Geiger counter

Scintillation counter

Radiotracers

Objective 10: State the basic assumptions made when using radiometric dating to determine the age of objects.

Objective 11: Calculate and predict the potential age of an object based on levels of concentration or C-14 within that sample or based on the given isotope ratio.

Objective 11 Example

Objective 11 Practice

Objective 13: Calculate the energy or mass change in a nuclear reaction, given one of these quantities.

Energy Change in Nuclear Reactions

Objective 13 Example

Objective 13 Practice

Objective 14: Calculate the mass defect, total nuclear binding energy, and binding energy per nucleon for a nuclide given its nuclear or atomic mass and the masses for protons, electrons and neutrons.

Mass Defect and Binding Energy

Objective 14 example:

Binding Energy Curve

Objective 15: Distinguish between fission and fusion and state what type of nuclei will undergo these processes.

Objective 16: Based on the plot of binding energy/nucleon versus mass number, predict whether isotopes would react via fusion or fission reactions.

Binding energy for various nuclides and its role in nuclear reactions

Objective 17: Identify and balance nuclear equations for fission and fusion reactions.

Objective 18: Briefly describe the general design of a nuclear reactor.

Objective 19: State the purpose of the fuel rods, control rods, moderator and cooling fluid in nuclear reactors.

Objective 20: Identify the advantages of a fusion reactor over a fission reactor and explain the problems with using nuclear reactors as energy sources.

Nuclear reactors

Objective 7: Predict whether a nuclide is likely to be stable or unstable (radioactive). If unstable, predict the most likely mode of decay to achieve stability. (For example, explain why tritium, ³H, is unstable.)